Warning : This document is still a draft
Information Theory Cheat Sheet
Here we (try to) explain and illustrate information theory common formula.
Introduction
Information Theory is an old topic, still useful, but tends to be forgotten. The idea of this article is to summarize the main formula, give them an interpretation.
Illustration of the Problem
In computer science, we often focus on efficiency, how to reduce the memory/computing/storage/communication cost. Here, information theory is about efficient memory, so it includes storage and exchange, where you want to optimize your bandwidth, the RAM or disk space needed.
We first need to describe the space, the problem we want to optimize. We cannot optimize for the unknown, we need to define first the finite set of symbols we want to exchange. Usually, this can be a set of values, letters, words, or abstract symbols.
No Encoding
Suppose you want to play Shifumi (Paper, Rock, Scissors).
At each round, you send to a server which item you selected.
Without optimization, Paper costs 5 bytes, Rock 4 bytes, and Scissors 8 bytes (each symbol encoded with ASCII 1 \(\times\) the word length).
Assuming that each symbol is selected at random, on average, we send \(\frac{1}{3}(5 + 4 + 8) \approx 5.7\) bytes.
Binary encoding
The minimal unit in a computer is a bit, which can be either \(0\) or \(1\) (1 byte = 8 bits). Rather than encoding with a string the decision for the round, a much more efficient scheme is to encode the result over 2 bits.
We would have:
00corresponding toPaper10corresponding toRock01corresponding toScissors
This is much better, and on average, we would need \(2\) bits per action.
Compared to the previous situation, we reduced by \(23\) the amount of information exchanged.
Here, you see that the code 11 is not used. So the efficiency can still be improved.
The maximum number of bits necessary in the general case for an alphabet of symbols \(\mathcal{X}\) which are identically distributed is simply calculated as:
\[\log_2(|\mathcal{X}|)\]This formula comes from \(H(X) = - \sum P(X)\log_2(P(X)) = \sum \frac{1}{\vert\mathcal{X}\vert} \log_2 \vert\mathcal{X}\vert= \frac{\vert\mathcal{X}\vert}{\vert\mathcal{X}\vert} \log_2 \vert\mathcal{X}\vert\),
when all events \(P(X) = \frac{1}{\vert\mathcal{X}\vert}\) have the same probability.
Optimal Encoding
In the current example, you can see that the code 11 is not used, leading to inefficiency of the encoding (well, it is still better than the string encoding).
Here comes Huffman’s trees which provides non ambiguous codes:
0corresponding toPaper10corresponding toRock11corresponding toScissors
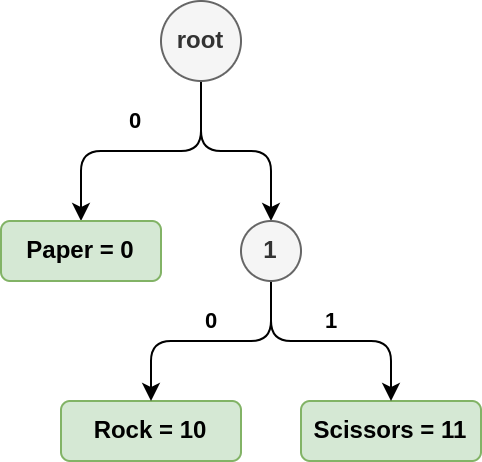
When we look at the string 01011011, there is a single unique way to read it:
0: Paper10: Rock11: Scissors0: Paper11: Scissors
Given the codes [0, 10, 11], we need \(\frac{1 + 2 + 2}{3} \approx 1.7\) bits to encode the message.
Information theory can be seen as a tool to compare encoding/compression and compares it to the theoretical bound. In this case where we have \(3\) elements, the theoretical lower bound is \(1.58\) bits \(\log_2(3)\). If we had \(4\) elements, the theoretical bound would have been \(2\), and therefore the binary encoding would have been optimal.
This is the end of our introduction. The rest of the article will describe and explain the main formulas.
This article must be used as a “Cheat Sheet”. There is no story or goal, this is just a bunch of formulas explained, where the relationship between the current one and the next one does not necessarily exists.
Table of Content
TODO
- [Introduction]
- [Basic formula]
- [InfoTheory in the real world]
Main Formulas
Notation
- \(X\): a random discrete variable
- \(\mathcal{X}\): the set of values taken by \(X\)
- \(x\): a realization of \(X\), with \(x \in \mathcal{X}\)
- \(x_i\): the \(i\)-est realization of \(X\)
- \(\mathbf{x}\) is a collection of successive observation
- \(P(X=x) = P(x)\): The probability of \(X\) taking the value \(x\)
Example with a Dice
This example helps to get a better idea of the quantities presented in the notation paragraph.
A dice with \(6\) faces is represented by the random (discrete) variable \(X\).
Outcomes: We have \(6\) possible outcomes: \(\mathcal{X} = \{1, 2, 3, 4, 5, 6\}\)
- If I launch the dice once and get \(4\), then \(x=4\).
- If I launch the dice three times, I get \(6\), then \(2\) then \(5\), then \(\mathbf{x} = [6, 2, 5]\) and $x_1 = 6, x_2=2, x_3=5$$.
Probabilities:
- If I have a normal dice, \(P(X=1) = P(X=2) = ... = P(X=6) = \frac{1}{6}\).
- If I have a loaded dice, the equality doesn’t hold, because some numbers are more likely.
Shannon Entropy
The entropy is the major concept of information theory. The entropy of a random variable \(X\) is denoted \(H(X)\). It represents the average amount of bits necessary to convey one element of information.
The formula is:
\[H(X) = - \sum_{x \in \mathcal{X}} P(X=x) \log_2 P(X=x)\]In this formula, we use the logarithm in base \(2\). Therefore, it represents bits. It is possible to use the Neperian logarithm \(\ln\) (in base \(e\)). In that case, we talk about nats. Nats are almost never used, so when talking about entropy, \(\log\) implicitly means \(\log_2\) for conciseness.
Boundaries
The minimal value is \(0\), where there is no information (we get always the same outcome).
Note: If you are in a communication, the number of symbols exchanged does not count ! (nor the date you receive it). This is only for describing the content.
The maximal value is \(\log_2 \mid\mathcal{X}\mid\), when the information cannot be compressed. As elements are uniformly distributed, no symbol is more likely than another.
Examples
Normal Dice
We have \(P(X=i) = \frac{1}{6}\). If we replace in the formula, we have:
\[H(X) = - \sum_{i=1}^6 P(X=i) \log_2 P(X=i) = - \sum_{i=1}^6 \frac{1}{6} \log_2 \frac{1}{6} = \frac{1}{6} \sum_{i=1}^6 \log_2(6) = \log_2(6) \approx 2.585\]Loaded Dice
Suppose we have the following probability table:
| \(P(X=1)\) | \(P(X=2)\) | \(P(X=3)\) | \(P(X=4)\) | \(P(X=5)\) | \(P(X=6)\) |
|---|---|---|---|---|---|
| 1/12 | 3/12 | 1/12 | 3/12 | 1/12 | 3/12 |
The formula become:
\[H(X) = 3 \frac{\log_2(12)}{12} + 3 \times 3 \frac{\log_2(12) - \log_2(3)}{12} = \frac{1}{12}\left(12\log_2(12) - 9 \log_2(3)\right)\] \[=\log_2(3 \times 4) - \frac{3}{4} \log_2(3) = \log_2(4) + \frac{1}{4}\log_2(3) \approx 2.396\]You can see that less bits are necessary (compared to the normal dice), but the drop is very limited.
Deterministic Dice
Suppose that \(P(X=6) = 1\), and \(P(X=i) = 0\) for all \(i \neq 6\). Then, we have:
\[H(X) = - 1 \log_2(1) - 5 \times 0 \log_2(0) = 0\]Well, no surprise ?
Join Entropy
When you have two categorical variables observed at the same time, you can compute the join entropy.
The entropy is the average amount of bits necessary to send the two information together. The join entropy is the generalization to a pair of variables.
The formula is simply:
\[H(X, Y) = -\sum_{x \in \mathcal{X}, y \in \mathcal{Y}} P(X=x, Y=y) \log P(X=x, Y=y)\]This is as if categories of variable \(X\) and \(Y\) where coalesced together. For instance, if \(\mathcal{X} = \{a, b, c\}\) and \(\mathcal{Y} = \{u, v\}\), we can construct \(Z\) such as \(\mathcal{Z} = \{(a, u), (b, u), (c, u), (a, v), (b,v), (c,v)\}\). \(H(Z)\) is equal to \(H(X, Y)\).
Note that \(P(Z=(a, u)) = P(X=a, Y=u) \neq P(X=a)P(Y=u)\) unless \(X\) and \(Y\) are independent.
Extension to \(n\) variables
The join entropy can be generalized to \(n\) variables:
\[H(X_1, X_2, ..., X_n) = -\sum_{x_1 \in \mathcal{X}_1, x_1 \in \mathcal{X}_2, ..., x_n \in \mathcal{X}_n} P(X_1=x_1, X_2=x_2, ..., X_n=x_n) \log P(X_1=x_1, X_2=x_2, ..., X_n=x_n)\]Boundaries
The join entropy is bounded by \(0\) and \(H(X) + H(Y)\).
- The lower bound can only be equal to \(0\) if \(H(X) = H(Y) = 0\).
- The upper bound is maximal if the two random variables \(X\) and \(Y\) are independent.
Useful Property
Symmetry
\[H(X, Y) = H(Y, X)\]Conditional Entropy
The conditional entropy is the additional amount of bits necessary to send \(Y\) when we have already sent \(X\).
We have a simple relationship between conditional entropy \(H(X \mid Y)\) and the previously defined entropy:
\[H(Y \mid X) = H(X, Y) - H(X)\]If we do not want to compute \(H(X, Y)\), the formula is:
\[H(Y | X) = - \sum_{x \in \mathcal{X}, y \in \mathcal{Y}} P(X=x, Y=y) \log_2 \frac{P(X=x, Y=y)}{P(X=x)}\]Useful Property:
Chain rule
\[H(X, Y) = H(X | Y) + H(Y)\]Can be generalized to more variables:
\[H(X, Y, Z) = H(X, Y | Z) + H(Z) = H(X | Y, Z) + H(Y | Z) + H(Z)\]Generalization of the Chain rule
\[H(X_1, X_2, ..., X_n) = \sum_i H(X_i | X_1, ..., X_{i-1})\]Mutual Information (MI)
This is the amount of information shared by two random variables. This is highly related to the join entropy. This can be seen as the amount of bits saved when sending \(X\) and \(Y\) together.
\[I(X, Y) = H(X) + H(Y) - H(X, Y)\]In this formula, the mutual information can be seen as the gain when sending \(X\) and \(Y\) together VS when they are sent separately.
The direct formula using probability terms is:
\[I(X, Y) = \sum_{x \in \mathcal{X}, y \in \mathcal{Y}} P(X=x, Y=y) \log \frac{P(X=x, Y=y)}{P(X=x)P(Y=y)}\]If we already have the entropy and the conditional one, we can compute the mutual information as:
\[I(X, Y) = H(X) - H(X|Y)\]or similarly
\[I(X, Y) = H(Y) - H(Y | X)\]\(H(X \vert Y)\) represents the information that \(Y\) cannot explain, which is subtracted to the information contained in \(X\).
Boundaries
\[0 \leq I(X, Y)\leq \min(H(X), H(Y))\]\(I(X, Y) = 0\) when \(X\) and \(Y\) are independent.
\(I(X, Y) \leq \min(H(X), H(Y))\): the maximal amount of shared information is the lowest entropy. If \(H(X) < H(Y)\), then \(X\) is “coarse” compared to \(Y\) and cannot explain more.
Other
\[I(X; Y) = KL(p(X, Y)\| p(X)p(Y))\]There is the Adjusted Mutual information 2, which takes into account “chance” in the cluster randomness…
\[AMI = \frac{MI - \mathbb{E}(MI)}{\frac{H(X) + H(Y)}{2} - \mathbb{E}(MI)}\]Cross Entropy
For the previous examples, for join or conditional entropy, \(X\) and \(Y\) do not share their alphabet.
\(X\) can be [Rock, Paper, Scissors], while \(Y\) can take value like [oval, round, square, triangle].
For cross entropy, \(X\) and \(X'\) share the same alphabet of symbols \(\mathcal{X} = \mathcal{X}'\). However, they do not necessarily have the same distribution, i.e., \(P(X=x) \neq P(X'=x)\).
\(X\) and \(X'\) may have their own best encoding, which minimize the amount of bits exchanged.
The cross entropy \(H^*(X, X')\) represents the average number of bits transmitted to transmit \(X\) if \(\mathbf{X}\) is encoded using the codebook of \(\mathbf{X}'\).
\[H^*(X, X') = - \sum_{x \in \mathcal{X}} P(X=x) \log_2 P(X'=x)\]Useful Properties
- Right addition
- Left addition
- Inversion
- Simple Entropy
- Arrival of a factor on the left
- Arrival of a factor on the right
Summary
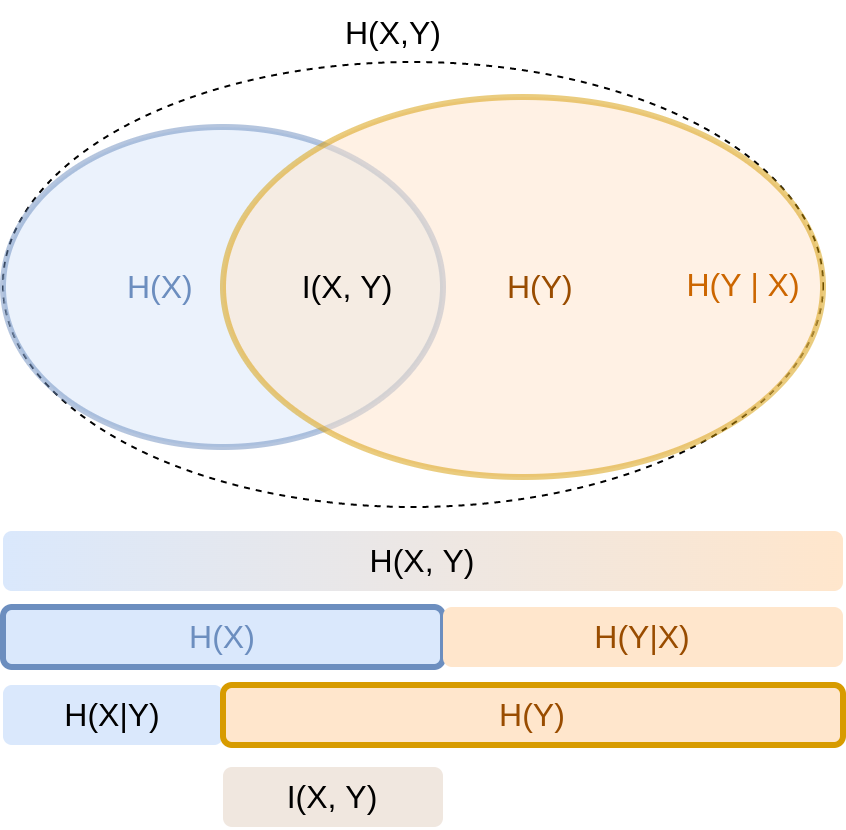
This diagram summarizes the relationships between the different quantities
Information Theory in Real World
CVR Consistency Violation Ratio
\[\frac{\hat{H}_T(T | X)}{\hat{H}(Y)}\]Normalized Mutual Information NMI
The NMI is simply the Normalized Information divided by its harmonic upper bound \(\frac{H(X) + H(Y)}{2}\).
\[NMI(X, Y) = 2 \times \frac{I(X, Y)}{H(X) + H(Y)}\]An alternative formula is:
\[NMI(X, Y) = 2 \times \frac{H(X, Y) - H(X) - H(Y)}{H(X) + H(Y)} = 2 \left(\frac{H(X, Y)}{H(X) + H(Y)} - 1\right)\]This indicator is often used to compare two clusterings or one classification to one clustering. The number of groups represented by each variable does not need to be equal. It measures the overlap between groups.
The value range in \([0, 1]\):
- \(1\) is the best value you can obtain (exact overlap of X’s clusters X with Y’s clusters).
- \(0\) is when clusters are completely random (you do not get an exact zero, but something very close)
\(V\)-Measure
The idea is similar to NMI, where it helps to compare one clustering \(K\) to a reference labeling \(C\).
In addition, there is a balance factor \(\beta\) which gives more priority to \(K\) or to \(C\) depending on the use case.
The \(V\)-measure is computed as:
\[\frac{(1 + \beta)\times h \times c}{\beta \times h + c}\]where:
- \(h\) is the homogeneity: A cluster must contain only items of a single class to be maximal,
- \(c\) is the completeness: All members of a given class must be grouped into a single cluster to be maximal.
- \(\beta \in [0, \infty[\) is the balance parameter, by default set to \(1\).
Homogeneity
\[h = 1 - \frac{H(C | K)}{H(C)}\]Where:
- \(H(C\|K)\): Conditional entropy of the class given cluster assignments,
- \(H(C)\): Entropy of the class given cluster assignments.
Completeness
The completeness is defined similarly, by just exchanging the role of \(C\) and \(K\).
\[c = 1 - \frac{H(K | C)}{H(K)}\]Divergence
The term “divergence” is the distance between two distributions having the same support.
Here, between two random variables \(X\) and \(X'\) sharing the same symbols \(\mathcal{X}\).
Kullback Leibler Divergence
The \(KL(X, X')\) divergence measures the inefficiency of sending \(X\) using the codebook of \(X'\)
This is the most common divergence, which is defined as:
\[D_{KL}(X \|X') = \sum_{x \in \mathcal{X}} P(X=x) \log \frac{P(X=x)}{P(X'=x)} = H^*(X, X') - H(X)\]As a reminder, the cross entropy is the cost of encoding \(X\) using the optimal codebook of \(X'\). Therefore, \(H^*(X, X') - H(X)\) is the difference between the optimal cost (\(H(X)\)) and the non-optimal one (\(H^*(X, X')\)).
The divergence is:
- equal to \(0\) if \(X\) and \(X'\) have the same distribution.
- infinite if \(X\) use at least one symbol \(x\) where \(P(X'=x) = 0\) (intuitively, there is no dedicated code for \(x\) in \(X'\), therefore it is impossible to encode \(x\)).
Useful ressources about symmetrization and other divergences
Jensen Shannon Divergence
The Kullback Leibler divergence is not symmetric, i.e., \(KL(P \| Q) \neq KL(Q \| P)\) in most cases.
The JSD is the symmetric version, parametrized by \(\alpha \in [0, 1]\). Plus, it has the advantage of having finite values, even if \(X\) and \(X'\) do not share all their alphabet.
\[JSD(P \|Q, \alpha) = \alpha KL(P \| M) + (1-\alpha) KL(Q \| M)\]with \(M = \alpha P + (1 - \alpha) Q\)
The values are bounded between:
\[0 \leq JSD \leq \log 2\]Note: \(P\) and \(Q\) are commonly used to describe KL and JSD. \(P\) can be seen as the distribution of \(X\) and \(Q\) as the distribution of \(X'\).
It can be generalized to more than one distribution \(P_i\) with proportion \(p_i\):
\[JSD_{\pi_1, ..., \pi_n}(P_1, ..., P_n) = H(\sum_{i=1}^n \pi_i P_i) - \sum_{i=1}^n \pi_i H(P_i)\]with \(M = \frac{\sum \pi_i P_i}{\sum \pi_i}\)
MDL: Minimum Description Length
The minimum description length is a measure used to select a model, where the optimal model is the one with the shortest description.
The usual formulation is the following:
\[L(D) = \min_{H \in \mathcal{H}} L(H) + L(D | H)\]where:
- \(H\) is an hypothesis, which here correspond to a model, a way to encode the information
- \(D\) is the data
The length of the data is equal to (the length of the model) + (the length necessary to encode the data using the model).
If you need a very large model to predict the data, it is not efficient. The MDL does not take into account the accuracy/performances of the models. However, when two models have comparable results, then we must select the one with the shortest description.
Entropy Rate of a Markov Chain
In a Markov Chain, there is a set of states, say \(d\) states. When in state \(i\), we have a probability to switch of state \(j\) with probability \(P_{i \rightarrow j}\), and a probability to stay on the current state \(P_{i \rightarrow i}\).
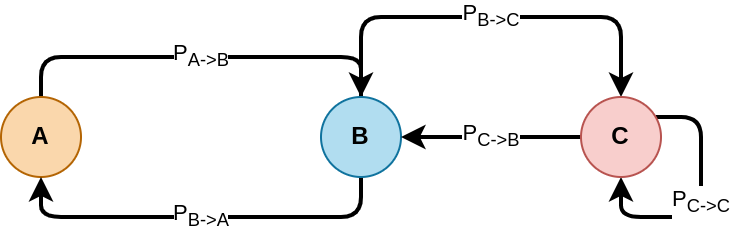
In the example above, we have the following joint probability table:
| \(P_{r \rightarrow c}\) | A |
B |
C |
|---|---|---|---|
A |
0 | \(P_{A\rightarrow B}\) | 0 |
B |
\(P_{B\rightarrow A}\) | 0 | \(P_{B\rightarrow C}\) |
C |
0 | \(P_{C\rightarrow B}\) | \(P_{C\rightarrow C}\) |
This specific structure has a defined entropy.
For each state (A, B and C in the previous figure), the “jump” probabilities sum to one, i.e., \(\sum_j P_{i \rightarrow j} = 1\)
To compute the entropy of a markov chain, it is “as if” computing the joint entropy \(H(A, B, C)\) up to a point.
In a Markov chain, after performing a large number of transitions, you reach a steady state, the asymptotic distribution where the probability of being on a state is stable. We denote this distribution \(\pmb{\mu}\) where \(\mu_A\) is the probability to be on state \(A\) after a large number of steps.
The entropy of the Markov chain is computed as:
\[H(\mathcal{X}) = - \sum_{i,j} \mu_i P_{i\rightarrow j} \log P_{i\rightarrow j}\]To be continued
Good introductive book 3.
Sources and Other Ressources
On Normalized Mutual Information: Measure Derivations and Properties
Useful ressources about symmetrization and other divergences
Wikipedia: Rate distortion theory
-
Cover, T. M., Thomas, J. A. (2006). Elements of Information Theory 2nd Edition (Wiley Series in Telecommunications and Signal Processing). Wiley-Interscience. ISBN: 0471241954 ↩
>> You can subscribe to my mailing list here for a monthly update. <<